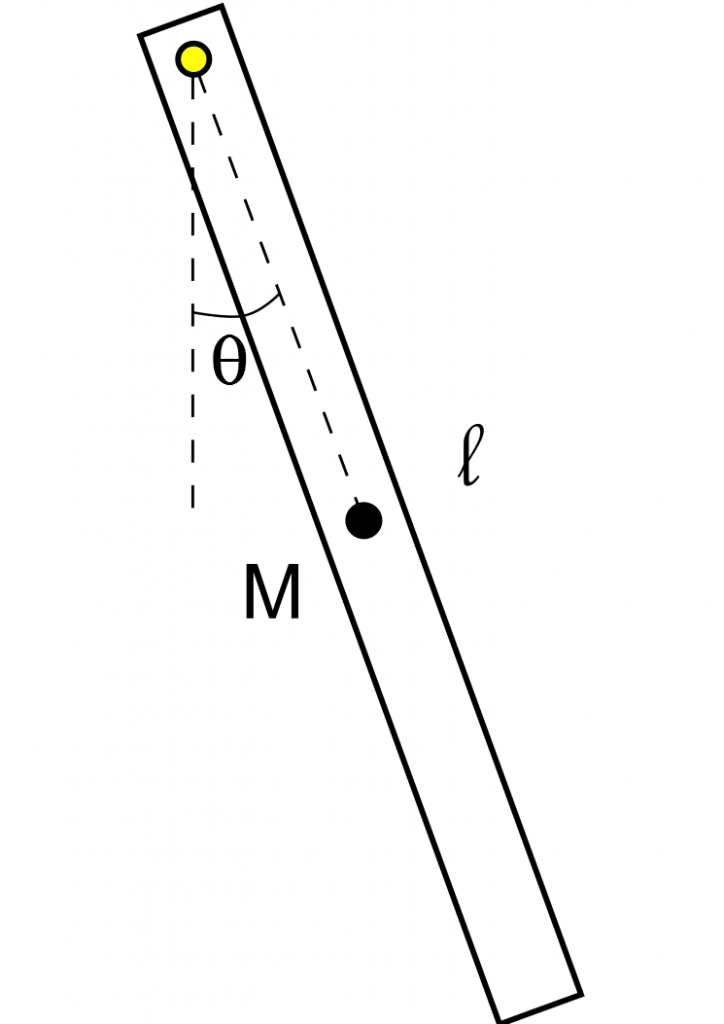
Rod of length ![]() and mass
and mass ![]() swinging about a pivot. First time using Inkscape, so I went and added
swinging about a pivot. First time using Inkscape, so I went and added ![]() , too.
, too.
I came across a slightly more advanced variation of this problem in a mechanics course earlier last semester, and for some reason I just couldn’t figure out how to find the kinetic energy. I found it instructive to go through a quick calculation…
The system is shown above – a simple rod swinging around a pivot that goes through one end. Assuming the usual things (the pivot at exactly the end of the rod, for example), there are two ways of finding the kinetic energy.
1. Shifting the Moment of Inertia
This is the classic way to approach this problem. Rotational kinetic energy is defined in terms of the moment of inertia about the pivot:
![]()
so we just use the parallel axis theorem to get the moment of inertia of a rod about its end,
![]()
where ![]() is just the distance between the center of mass and the pivot, and
is just the distance between the center of mass and the pivot, and ![]() can be easily found on Wikipedia, etc. or calculated. In fact,
can be easily found on Wikipedia, etc. or calculated. In fact, ![]() is also readily available, but whatever.
is also readily available, but whatever.
Going through the calculation gives us
![]()
which yields
![]()
2. Center of Mass Velocity
If you can’t use the parallel axis theorem (rare), the other method would be to decompose the kinetic energy into two parts: translational kinetic energy of the center of mass plus rotational kinetic energy of the rod about the center of mass. This is the same process used when calculating the kinetic energy of a spinning and translating rod (common problem in basic mechanics), for example. Thus, we write
![]()
where ![]() is the same as above, and the velocity of the center of mass is just
is the same as above, and the velocity of the center of mass is just
![]()
or in other words, the angular velocity of the rod ![]() times the distance from the pivot to the center of mass. As expected, this gives the same result
times the distance from the pivot to the center of mass. As expected, this gives the same result
![]()
To be honest, this inaugural post was written partly because I wanted to play with LaTeX/Inkscape and partly to get something onto my blog so it wouldn’t look this shabby anymore.
Hey, I don’t know if this has been mentioned or maybe it’s a subtlety I’m missing, but should your final equation for T also have a theta dot squared term on there as well? You didn’t put it in either equation.
Justin, you’re 100% correct. Fixed, thanks!
Hi if any one could help me on this. I need to know how to find the kinetic energy of a triple inverted pendulum for my project. Anyone can help with that? Thanks.
Hope your project went well.
While I can’t help the past you, I can still write something here:
Working through the triple pendulum isn’t any more difficult conceptually than a double pendulum (see: Wikipedia), and the inverted part means you’re choosing the unstable equilibrium point at the top and maybe adding some drive to stabilize it there. Unfortunately it’s still more work than I want to do.
On the other hand, I just want to remark that the double (and triple) pendulum system seems like a very simple model (it’s just the simple pendulum, but two of them, right?), but it carries a lot of interesting physics. For one, it’s chaotic, meaning that a tiny change in initial conditions causes huge variations in the behavior. Dropping the pendulum from some angle could result in boring motion looking like one long pendulum, or it could have some oscillations between the two pendulums, or it could go wild and spin around seemingly at random. Relevant video: https://www.youtube.com/watch?v=QXf95_EKS6E