Here’s my skin-deep understanding of the negative Kelvin temperatures mentioned in this article.
I took a statistical mechanics course last semester, and we learned that temperature is defined as:
![]()
where ![]() is energy and
is energy and ![]() is entropy, or a measure of how many possible arrangements are available given a certain total energy. A positive temperature implies that a small positive change in energy causes a small positive change in entropy. In other words, adding a little bit more energy to a system causes there to be more ways to get that energy.
is entropy, or a measure of how many possible arrangements are available given a certain total energy. A positive temperature implies that a small positive change in energy causes a small positive change in entropy. In other words, adding a little bit more energy to a system causes there to be more ways to get that energy.
We almost always observe positive temperatures because normally, there are a huge number of possible energy levels for a system (infinite, actually). Adding a bit of energy allows the system to tap into previously inaccessible energy levels. This increases the number of possible ways we can rearrange the atoms in the energy levels to obtain the total energy. Thus, the entropy increases.
So then to have a negative temperature, we need to have a system where adding a bit of energy decreases the entropy. Luckily, there are some systems we can build that have very few energy levels. Let’s take, for example, a system of ![]() particles with only two energy levels: a ground state (zero energy) and an excited state with energy
particles with only two energy levels: a ground state (zero energy) and an excited state with energy ![]() .
.
Say we want the system to have an overall energy of 0. There is only one possible way to arrange the particles to get a total energy of 0, and that’s to put them all in the ground state. In other words, there’s only one available microstate for the system.
Next, we bump up the energy just a bit, to ![]() . There’s only one way to get this total energy, and that’s to have one particle in the excited state with energy
. There’s only one way to get this total energy, and that’s to have one particle in the excited state with energy ![]() and the other
and the other ![]() particles without any energy. But wait – we can choose any of the particles to be the one in the excited state. Thus, we have
particles without any energy. But wait – we can choose any of the particles to be the one in the excited state. Thus, we have ![]() possible arrangements to get
possible arrangements to get ![]() .
.
You see that by giving a positive change to the energy, we have increased the entropy from zero to ![]() . But this isn’t all. If we keep on adding little bits of energy
. But this isn’t all. If we keep on adding little bits of energy ![]() , we will reach a point where the entropy levels off. From some mathy arguments, we can discover that the system has maximum entropy when
, we will reach a point where the entropy levels off. From some mathy arguments, we can discover that the system has maximum entropy when ![]() , or when we can put half of the particles in the ground state and half in the excited state. On second thought, let’s go into the mathy argument, since it’s not that bad.
, or when we can put half of the particles in the ground state and half in the excited state. On second thought, let’s go into the mathy argument, since it’s not that bad.
For ![]() , we need to pick one particle out of
, we need to pick one particle out of ![]() particles to be the one in the excited state. There are then
particles to be the one in the excited state. There are then ![]() number of possible ways to choose one particle.
number of possible ways to choose one particle.
For ![]() , we need to pick two particles out of
, we need to pick two particles out of ![]() particles to be in the excited state. We could naively say that there are
particles to be in the excited state. We could naively say that there are ![]() possible ways to pick the first particle and then
possible ways to pick the first particle and then ![]() ways to pick the second. However, since we don’t care about the order we choose the particles, two choices that could have been (particle #1) + (particle #2) and (particle #2) + (particle #1) are the same. That is, we overcount by two. Thus, there are
ways to pick the second. However, since we don’t care about the order we choose the particles, two choices that could have been (particle #1) + (particle #2) and (particle #2) + (particle #1) are the same. That is, we overcount by two. Thus, there are ![]() possible ways to choose two particles.
possible ways to choose two particles.
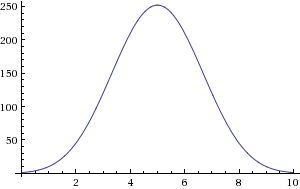
And so on, and so forth. It turns out that mathematicians had studied this “choosing k out of N” thing way back in the 1600s, and they named it the binomial coefficient, or written out, ![]() . The lumpy picture above is
. The lumpy picture above is ![]() plotted as a function of
plotted as a function of ![]() .
.
But back to negative temperature. Here, the energy essentially dictates how many particles we choose, and the entropy is proportional to the number of ways we can choose the particles, or the binomial coefficient plotted above: ![]() . Thus, we see that entropy maxes out smack dab in the middle where
. Thus, we see that entropy maxes out smack dab in the middle where ![]() , and the curve goes downhill past this point. This means that the slope
, and the curve goes downhill past this point. This means that the slope ![]() goes below zero – adding a small bit of energy causes the entropy to decrease.
goes below zero – adding a small bit of energy causes the entropy to decrease.
Voila. Negative temperature.
P.S.: The article and Wikipedia both mention that negative temperature is actually hotter than infinite temperature. We can see this from the binomial coefficient. The slope of the entropy curve goes to zero when entropy is maximized: ![]() . Temperature is the reciprocal of this, so we see that at the peak, temperature is infinity. Below this point, temperature is positive since the slope is positive. Above this point, temperature becomes negative. Thus, we see that negative temperatures are actually higher than positive temperatures.
. Temperature is the reciprocal of this, so we see that at the peak, temperature is infinity. Below this point, temperature is positive since the slope is positive. Above this point, temperature becomes negative. Thus, we see that negative temperatures are actually higher than positive temperatures.